GCE Advanced Level Maths Curriculum For 11th Grade And 12th Grade / GCE A LevelOur Singapore Maths books for 11th Grade And 12th Grade / GCE A Level are written in English and based on GCE A Level Maths curriculum for 11th Grade And 12th Grade / GCE A Level, which covers the following topics. If your child uses our Singapore Maths books for 11th Grade And 12th Grade / GCE A Level, he will be able to: Pure mathematics -
Functions and graphs - understand the terms function, domain, range and one-one function
- find composite functions and inverses of functions, including conditions for their existence
- understand and use the relation (fg)-1 = g-1f-1 where appropriate
- illustrate in graphical terms the relation between a one-one function and its inverse
- understand the relationship between a graph and an associated algebraic equation, and in particular show familiarity with the forms of the graphs of:
- y = kxn where n is a positive or negative integer or a simple rational number
- ax + by = c
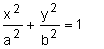 (knowledge of geometrical properties of conics is not required) (knowledge of geometrical properties of conics is not required) - understand and use the relationships between the graphs of y = f(x), y = af(x), y = f(x) + a, y = f(x+a), y = f(ax), where a is a constant, and express the transformations involved in terms of translations, reflections and scalings
- relate the equation of a graph to its symmetries
- understand, and use in simple cases, the expression of the coordinates of a point on a curve in terms of a parameter
-
Partial fractions - recall an appropriate form for expressing rational functions in partial fractions, and carry out the decomposition, in cases where the denominator is no more complicated than:
- (ax + b)(cx + d)(ex + f)
- (ax + b)(cx + d)2
- (ax + b)(x2 + c2)
- including cases where the degree of the numerator exceeds that of the denominator
-
Inequalities; the modulus function - use properties of inequalities, and in particular understand that x > y and z > 0 imply that xz > yz while x > y and z < 0 imply xz < yz
- find the solution set of inequalities that are reducible to the form f(x) > 0, where f(x) can be factorised, and illustrate such solutions graphically
- understand the meaning of |x| and sketch the graph of functions of the form y = lax+ b|
- use relations such as lx - al < b
 a - b < x < a + b and |al = |b| a - b < x < a + b and |al = |b|  a2 = b2 in the course of solving equations and inequalities a2 = b2 in the course of solving equations and inequalities -
Logarithmic and exponential functions - recall and use the laws of logarithms (including change of base) and sketch graphs of simple logarithmic and exponential functions
- recall and use the definition ax = ex ln a
- use logarithms to solve equations reducible to the form ax = b, and similar inequalities
-
Sequences and series - understand the idea of a sequence of terms, and use notations such as un to denote the nth term of a sequence
- recognise arithmetic and geometric progressions
- use formulae for the nth term and for the sum of the first n terms to solve problems involving arithmetic or geometric progressions
- recall the condition for convergence of a geometric series, and use the formula for the sum to infinity of a convergent geometric series
- use
 notation notation - use the binomial theorem to expand (a + b)n, where n is a positive integer
- use the binomial theorem to expand (1 + x)n, where n is rational, and recall the condition |x|< 1 for the validity of this expansion
- recognise and use the notations n! (with 0! = 1) and
 -
Permutations and combinations - understand the terms 'permutation' and 'combination'
- solve problems involving arrangements (of objects in a line or in a circle), including those involving
- repetition (e.g. the number of ways of arranging the letters of the word NEEDLESS)
- restriction (e.g. the number of ways several people can stand in a line if 2 particular people must - or must not - stand next to each other)
-
Trigonometry - use the sine and cosine formulae
- calculate the angle between a line and a plane, the angle between two planes, and the angle between two skew lines in simple cases
-
Trigonometrical functions - understand the definition of the six trigonometrical functions for angles of any magnitude
- recall and use the exact values of trigonometrical functions of
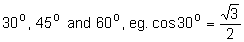 - use the notations sin-1x, cos-1x and tan-1x to denote the principal values of the inverse trigonometrical relations
- relate the periodicity and symmetries of the sine, cosine and tangent functions to the form of their graphs, and use the concepts of periodicity and / or symmetry in relation to these functions and their inverses
- use trigonometrical identities for the simplification and exact evaluation of expressions, and select an identity or identities appropriate to the context, showing familiarity in particular with the use of:
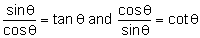 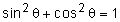 and equivalent statements and equivalent statements- the expansion of sin(A ± B), cos(A ± B) and tan(A + B)
- the formulae for sin2A, cos2A and tan2A
- the formulae for sin A ± sin B and cos A ± cos B
- the expression of a
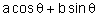 in the forms in the forms 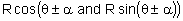 - find the general solution of simple trigonometrical equations, including graphical interpretation
- use the small-angle approximations
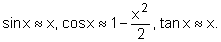 -
Differentiation - understand the idea of a limit and the derivative defined as a limit, including geometrical interpretation in terms of the gradient of a curve at a point as the limit of the gradient of a suitable sequence of chords
- use the standard notations
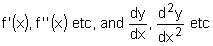 for derived functions for derived functions - use the derivatives of xn (for any rational n), sin x, cos x, tan x, ex, ax, ln x, sin-1x, cos-1x and tan-1x; together with constant multiples, sums, differences, products, quotients and composites
- find and use the first derivative of a function which is defined implicitly or parametrically
- locate stationary points, and distinguish between maxima, minima and stationary points of inflexion (knowledge of conditions for general points of inflexion is not required)
- find equations of tangents and normals to curves, and use information about gradients for sketching graphs
- solve problems involving maxima and minima, connected rates of change, small increments and approximations
- derive and use the first few terms of the Maclaurin series for a function
-
Integration - understand indefinite integration as the reverse process of differentiation
- integrate xn (including the case where n = -1), ex, sin x, cos x, sec2x, together with
- sums, differences and constant multiples of these
- expressions involving a linear substitution (e.g. e2x-1)
- applications involving the use of partial fractions
- applications involving the use of trigonometrical identities (e.g.
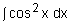 ) ) - recognise an integrand of the form
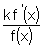 and integrate, e.g. and integrate, e.g. 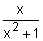 or tan x or tan x - integrate
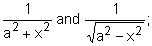 - recognise when an integrand can usefully be regarded as a product, and use integration by parts to integrate, e.g., x sin 2x, x2ex, ln x
- use the in method of integration by substitution to simplify and evaluate either a definite or an indefinite integral (including simple cases in which the candidates have to select the substitution themselves, e.g.
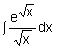 ) ) - evaluate definite integrals (including e.g.
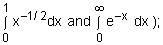 - understand the idea of the area under a curve as the limit of a sum of the areas of rectangles and use simple applications of this idea
- use integration to find plane areas and volumes of revolution in simple cases
- use the trapezium rule to estimate the values of definite integrals, and identify the sign of the error in simple cases by graphical considerations
-
Vectors - use rectangular cartesian coordinates to locate points in three dimensions, and use standard notations for vectors, i.e.
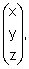 xi + yj + zk, a xi + yj + zk, a - carry out addition and subtraction of vectors and multiplication of a vector by a scalar, and interpret these operations in geometrical terms
- use unit vectors, position vectors and displacement vectors
- recall the definition of and calculate the magnitude of a vector and the scalar product of two vectors
- use the scalar product to determine the angle between two directions and to solve problems concerning perpendicularity of vectors
- understand the significance of all the symbols used when the equation of a straight line is expressed in either of the forms r = a + tb and
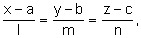 and convert equations of lines from vector to Cartesian form and vice versa and convert equations of lines from vector to Cartesian form and vice versa - solve simple problems involving finding and using either form of the equation of a line
- use equations of lines to solve problems concerning distances, angles and intersections, and in particular:
- determine whether two lines are parallel, intersect or are skew, and find the point of intersection of two lines when it exists
- find the perpendicular distance from a point to a line
- find the angle between two lines
- use the ratio theorem in geometrical applications
-
Mathematical induction - understand the steps needed to carry out a proof by the method of induction
- use the method of mathematical induction to establish a given result e.g. the sum of a finite series, or the form of an nth derivative
-
Complex numbers - understand the idea of a complex number, recall the meaning of the terms 'real part', 'imaginary part', 'modulus', 'argument', 'conjugate', and use the fact that two complex numbers are equal if and only if both real and imaginary parts are equal
- carry out operations of addition, subtraction, multiplication and division of two complex numbers expressed in cartesian form (x + iy)
- recall and use the relation zz* = |z|2
- use the result that, for a polynomial equation with real coefficients, any non-real roots occur in conjugate pairs
- represent complex numbers geometrically by means of an Argand diagram
- carry out operations of multiplication and division of two complex numbers expressed in polar form (
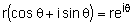 ) ) - understand in simple terms the geometrical effects of conjugating a complex number and of adding, subtracting, multiplying, dividing two complex numbers
- illustrate simple equations and inequalities involving complex numbers by means of loci in an Argand diagram (e.g.|z - a| < k, |z - a| = |z - b|, arg(z - a) =
 , but excluding arg(z-a)-arg(z-b) = ) , but excluding arg(z-a)-arg(z-b) = ) -
Curve sketching - understand the relationships between the graphs of y = f(x), y2 = f(x) and y = |f(x)|
- determine, in simple cases, the equations of asymptotes parallel to the axes
- use the equation of a curve, in simple cases, to make deductions concerning symmetry or concerning any restrictions on the possible values of x and / or y that there may be
- sketch curves of the form y = f(x), y2 = f(x) or y = |f(x)| (detailed plotting of curves will not be required, but sketches will generally be expected to show significant features, such as turning points, asymptotes and intersections with the axes)
-
First order differential fquations - formulate a simple statement involving a rate of change as a differential equation, including the introduction if necessary of a constant of proportionality
- find by integration a general form of solution for a first order differential equation in which the variables are separable
- find the general solution of a first order linear differential equation by means of an integrating factor
- reduce a given first order differential equation to one in which the variables are separable or to one which is linear by means of a given simple substitution
- understand that the general solution of a differential equation is represented in graphical terms by a family of curves, and sketch typical members of a family in simple cases
- use an initial condition to find a particular solution to a differential equation, and interpret a solution in terms of a problem modelled by a differential equation
-
Numerical methods - locate approximately a root of an equation by means of graphical considerations and / or searching for a sign change
- use the method of linear interpolation to find an approximation to a root of an equation
- understand the idea of, and use the notation for, a sequence of approximations which converges to the root of an equation
- understand how a given simple iterative formula of the form
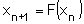 relates to the equation being solved, and use a given iteration to determine a root to a prescribed degree of accuracy (conditions for convergence are not included) relates to the equation being solved, and use a given iteration to determine a root to a prescribed degree of accuracy (conditions for convergence are not included) - understand, in geometrical terms, the working of the Newton-Raphson method, and derive and use iterations based on this method
- appreciate that an iterative method may fail to converge to the required root
Particle mechanics -
Forces and equilibrium - identify the forces acting in a given situation
- understand the representation of forces by vectors, and find and use resultants and components
- solve problems concerning the equilibrium of a particle under the action of coplanar forces (using equations obtained by resolving the forces, or by using a triangle or polygon of forces)
- recall that the contact force between two surfaces can be represented by two components (the 'normal component' and the 'frictional component') and use this representation in solving problems
- use the model of a 'smooth' contact and understand the limitations of this model
- understand the concept of limiting friction and limiting equilibrium, recall the definition of coefficient of friction; and use the relationship
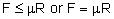 as appropriate (knowledge of angle of friction will not be required) as appropriate (knowledge of angle of friction will not be required) - recall and use Newton's third law
-
Kinematics of motion in a straight line - understand the concepts of distance and speed, as scalar quantities, and of displacement, velocity and acceleration, as vector quantities, and understand the relationships between them
- sketch and interpret x-t and v-t graphs, and in particular understand and use the facts that:
- the area under a v-t graph represents displacement
- the gradient of an x-t graph represents velocity
- the gradient of a v-t graph represents acceleration
- use appropriate formulae for motion with constant acceleration in a straight line
-
Newton's laws of motion - recall and use Newton's first and second laws of motion
- apply Newton's laws to the linear motion of a particle of constant mass moving under the action of constant forces (including friction)
- solve problems on the motion of two particles, connected by a light inextensible string which may pass over a fixed smooth light pulley or peg
-
Energy, work and power - understand the concept of the work done by a force, and calculate the work done by a constant force when its point of application undergoes a displacement not necessarily parallel to the force (use of the scalar product is not required)
- understand the concepts of gravitational potential energy and kinetic energy, and recall and use appropriate formulae
- understand and use the relationship between the change in energy of a system and the work done by the external forces, and use where appropriate the principle of conservation of energy
- recall and use the definition of power as the rate at which a force does work, and use the relationship between power, force and velocity for a force acting in the direction of motion
- solve problems involving, for example, the instantaneous acceleration of a car moving on a hill with resistance
-
Linear motion under a variable force - solve simple problems on the linear motion of a particle of constant mass moving under the action of variable forces by setting up and solving an appropriate differential equation (use of
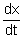 for velocity and for velocity and 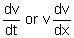 , as appropriate, for acceleration is expected, and any differential equations to be solved will be first order with separable variables) , as appropriate, for acceleration is expected, and any differential equations to be solved will be first order with separable variables) -
Motion of a projectile - model the motion of a projectile as a particle moving with constant acceleration, and understand the limitations of this model
- use horizontal and vertical equations of motion to solve problems on the motion of projectiles (including finding the magnitude and direction of the velocity at a given time or position and finding the range on a horizontal plane)
- derive and use the cartesian equation of the trajectory of a projectile, including cases where the initial speed and/or angle of projection is unknown (knowledge of the range on an inclined plane is not required)
-
Hooke's law - recall and use Hooke's law as a model relating the force in an elastic string or spring to the extension or compression, and understand and use the term 'modulus of elasticity'
- understand the concept of elastic potential energy, and recall and use the appropriate formula for its calculation
- use considerations of work and energy to solve problems involving elastic strings and springs
-
Uniform circular motion - understand the concept of angular speed for a particle moving in a circle with constant speed, and recall and use the relation
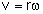 (no proof required) (no proof required) - understand that the acceleration of particle moving in a circle with constant speed is directed towards the centre of the circle and has magnitude
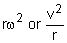 (no proof required) (no proof required) - use Newton's second law to solve problems which can be modelled as the motion of a particle moving in a circle with constant speed
Probability and statistics -
Probability - use addition and multiplication of probabilities, as appropriate, in simple cases, and understand the representation of events by means of tree diagrams
- understand the meaning of mutually exclusive and independent events, and calculate and use conditional probabilities in simple cases
- understand and use the notations P(A),
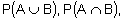 P(A|B) and the equations P(A|B) and the equations  and and 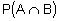 = P(A) P(B|A) = P(B) P(A|B) (the general form of Bayes' theorem is not required) = P(A) P(B|A) = P(B) P(A|B) (the general form of Bayes' theorem is not required) -
Discrete random variables - understand the concept of a discrete random variable
- construct a probability distribution table relating to a given situation, and calculate E(X) and Var(X)
- appreciate conditions under which a uniform distribution or a binomial distribution B(n,p) may be a suitable probability model, and recall and use formulae for the calculation of binomial probabilities
- understand conditions under which a Poisson distribution Po(
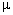 ) may be a suitable probability model, and recall and use the formula for the calculation of Poisson probabilities ) may be a suitable probability model, and recall and use the formula for the calculation of Poisson probabilities - recall and use the means and variances of binomial and Poisson distributions
- use a Poisson distribution as an approximation to a binomial distribution, where appropriate (candidates should know that the conditions n > 50 and np < 5, approximately, can generally be taken to be suitable)
-
The normal distribution - recall the general shape of a normal curve, and understand how the shape and location of the distribution
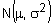 are affected by the values of are affected by the values of 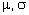 (in general terms only; no knowledge of mathematical properties of the normal density function is included) (in general terms only; no knowledge of mathematical properties of the normal density function is included) - standardise a normal variable and use normal distribution tables
- use the normal distribution as a probability model, where appropriate, and solve problems concerning a variable X, where
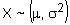 , including: , including: - finding the value of P(X < x1) given the values of
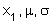 - use of the symmetry of the normal distribution
- finding a relationship between
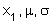 given the value of P(X < x1) given the value of P(X < x1) - repeated application of the above
- recall conditions under which a normal distribution may be used to approximate a binomial distribution (n sufficiently large to ensure that np > 5 and nq > 5. approximately) or Poisson distribution (
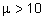 , approximately), and calculate such approximations, including the use of a continuity correction , approximately), and calculate such approximations, including the use of a continuity correction -
Samples - understand the distinction between a sample and a population, and appreciate the necessity for randomness in choosing samples
- explain in simple terms why a given sampling method may be unsatisfactory (a detailed knowledge of sampling and survey methods is not required)
- recognise that the sample mean can be regarded as a random variable, and use the facts that
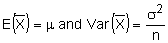 - use the fact that X is normally distributed if X is normally distributed
- use the Central Limit Theorem (without proof) to treat X as being normally distributed when the sample size is sufficiently large ('large' samples will usually be of size at least 50, but candidates should know that using the approximation of normality can sometimes be useful with samples that are smaller than this)
- calculate unbiased estimates of the population mean and population variance from a sample (only a simple understanding of the term 'unbiased' is required)
- determine, from a sample from a normal distribution of known variance or from a large sample, a confidence interval for the population mean
- determine, from a large sample, a confidence interval for a population proportion
-
Linear combinations of random variables - recall and use the results in the course of solving problems that, for either discrete or continuous random variables,
- E(aX + b) = aE(X) + b and Var(aX + b) = a2 Var(X)
- E(aX + bY) = aE(X) + bE(Y)
- Var(aX + bY) = a2 Var(X) + b2 for independent X and Y
- recall and use the results that:
- if X has a normal distribution then so does aX + b
- if X and Y have independent normal distributions then aX + bY has a normal distribution
- if X and Y have independent Poisson distributions then X + Y has a Poisson distribution
-
Continuous random variables - understand and use the concept of a probability density function, and recall and use the properties of a density function (which may be defined 'piecewise')
- use a given probability density function to calculate the mean, mode and variance of a distribution, and in general use the result
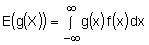 in simple cases, where f(x) is the probability density function of X and g(X) is a function of X in simple cases, where f(x) is the probability density function of X and g(X) is a function of X - understand and use the relationship between the probability density function and the distribution function and use either to evaluate the median, quartiles and other percentiles
- use a probability density function or a distribution function in the context of a model, including in particular the continuous uniform (rectangular) distribution
-
Hypothesis testing - understand and use the concepts of hypothesis (null and alternative), test statistic, significance level, and hypothesis test (1-tail and 2-tail)
- formulate hypotheses and apply a hypothesis test concerning the population mean using:
- a sample drawn from a normal distribution of known variance
- a large sample drawn from any distribution of unknown variance
- formulate hypotheses concerning a population proportion, and apply a hypothesis test using a normal approximation to a binomial distribution
Please enter a number in the Qty box next to the products that you want to order, and then click on the Add to cart button. To learn more about a product, please scroll down this page or click on its name, where applicable. |